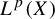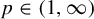1 results
Some remarks on oscillation inequalities
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 29 November 2022, pp. 3383-3412
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
-
In this paper, we establish uniform oscillation estimates on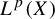
$L^p(X)$ with 
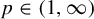$p\in (1,\infty )$ for the polynomial ergodic averages. This result contributes to a certain problem about uniform oscillation bounds for ergodic averages formulated by Rosenblatt and Wierdl in the early 1990s [Pointwise ergodic theorems via harmonic analysis. Proceedings of Conference on Ergodic Theory (Alexandria, Egypt, 1993) (London Mathematical Society Lecture Notes, 205). Eds. K. Petersen and I. Salama. Cambridge University Press, Cambridge, 1995, pp. 3–151]. We also give a slightly different proof of the uniform oscillation inequality of Jones, Kaufman, Rosenblatt, and Wierdl for bounded martingales [Oscillation in ergodic theory. Ergod. Th. & Dynam. Sys. 18(4) (1998), 889–935]. Finally, we show that oscillations, in contrast to jump inequalities, cannot be seen as an endpoint for r-variation inequalities.
