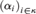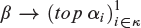Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
  1. Home
  2. Search

Refine search

Refine search

Access:
Content type:
Publication date:
Apply   From and To filters
Subject: Show more
Journals Show more
Publishers: Show more
Societies Show more
Series: Show more
Collections: Show more

Actions for selected content:

Select all | Deselect all
  • View selected items
  • Export citations
  • Download PDF (zip)
  • Save to Kindle
  • Save to Dropbox
  • Save to Google Drive

Save Search

You can save your searches here and later view and run them again in "My saved searches".

Please provide a title, maximum of 40 characters.
Cancel
×

1 results

  • THE TOPOLOGICAL PIGEONHOLE PRINCIPLE FOR ORDINALS

  • JACOB HILTON
  • Journal:
    The Journal of Symbolic Logic / Volume 81 / Issue 2 / June 2016
    Published online by Cambridge University Press:
    29 June 2016, pp. 662-686
    Print publication:
    June 2016

  • Given a cardinal κ and a sequence 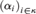${\left( {{\alpha _i}} \right)_{i \in \kappa }}$ of ordinals, we determine the least ordinal β (when one exists) such that the topological partition relation

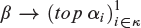    $$\beta \to \left( {top\,{\alpha _i}} \right)_{i \in \kappa }^1$$
    holds, including an independence result for one class of cases. Here the prefix “top” means that the homogeneous set must be of the correct homeomorphism class rather than the correct order type. The answer is linked to the nontopological pigeonhole principle of Milner and Rado.