The
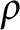 $\rho $
-Einstein soliton is a self-similar solution of the Ricci–Bourguignon flow, which includes or relates to some famous geometric solitons, for example, the Ricci soliton and the Yamabe soliton, and so on. This paper deals with the study of
$\rho $
-Einstein soliton is a self-similar solution of the Ricci–Bourguignon flow, which includes or relates to some famous geometric solitons, for example, the Ricci soliton and the Yamabe soliton, and so on. This paper deals with the study of
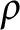 $\rho $
-Einstein solitons on Sasakian manifolds. First, we prove that if a Sasakian manifold M admits a nontrivial
$\rho $
-Einstein solitons on Sasakian manifolds. First, we prove that if a Sasakian manifold M admits a nontrivial
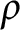 $\rho $
-Einstein soliton
$\rho $
-Einstein soliton
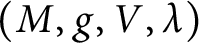 $(M,g,V,\lambda )$
, then M is
$(M,g,V,\lambda )$
, then M is
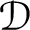 $\mathcal {D}$
-homothetically fixed null
$\mathcal {D}$
-homothetically fixed null
 $\eta $
-Einstein and the soliton vector field V is Jacobi field along trajectories of the Reeb vector field
$\eta $
-Einstein and the soliton vector field V is Jacobi field along trajectories of the Reeb vector field
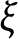 $\xi $
, nonstrict infinitesimal contact transformation and leaves
$\xi $
, nonstrict infinitesimal contact transformation and leaves
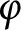 $\varphi $
invariant. Next, we find two sufficient conditions for a compact
$\varphi $
invariant. Next, we find two sufficient conditions for a compact
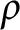 $\rho $
-Einstein almost soliton to be trivial (Einstein) under the assumption that the soliton vector field is an infinitesimal contact transformation or is parallel to the Reeb vector field
$\rho $
-Einstein almost soliton to be trivial (Einstein) under the assumption that the soliton vector field is an infinitesimal contact transformation or is parallel to the Reeb vector field
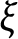 $\xi $
.
$\xi $
.
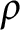 $\rho $
-Einstein solitons on Sasakian manifolds
$\rho $
-Einstein solitons on Sasakian manifolds