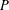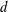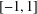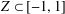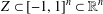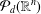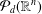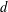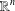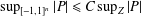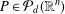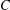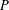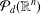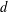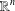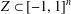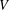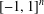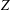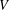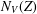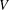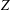The classical Remez inequality [‘Sur une propriété des polynomes de Tchebycheff’, Comm. Inst. Sci. Kharkov13 (1936), 9–95] bounds the maximum of the absolute value of a real polynomial 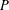 $P$ of degree
$P$ of degree 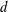 $d$ on
$d$ on 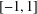 $[-1,1]$ through the maximum of its absolute value on any subset
$[-1,1]$ through the maximum of its absolute value on any subset 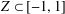 $Z\subset [-1,1]$ of positive Lebesgue measure. Extensions to several variables and to certain sets of Lebesgue measure zero, massive in a much weaker sense, are available (see, for example, Brudnyi and Ganzburg [‘On an extremal problem for polynomials of
$Z\subset [-1,1]$ of positive Lebesgue measure. Extensions to several variables and to certain sets of Lebesgue measure zero, massive in a much weaker sense, are available (see, for example, Brudnyi and Ganzburg [‘On an extremal problem for polynomials of  $n$ variables’, Math. USSR Izv.37 (1973), 344–355], Yomdin [‘Remez-type inequality for discrete sets’, Israel. J. Math.186 (2011), 45–60], Brudnyi [‘On covering numbers of sublevel sets of analytic functions’, J. Approx. Theory162 (2010), 72–93]). Still, given a subset
$n$ variables’, Math. USSR Izv.37 (1973), 344–355], Yomdin [‘Remez-type inequality for discrete sets’, Israel. J. Math.186 (2011), 45–60], Brudnyi [‘On covering numbers of sublevel sets of analytic functions’, J. Approx. Theory162 (2010), 72–93]). Still, given a subset 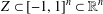 $Z\subset [-1,1]^{n}\subset \mathbb{R}^{n}$, it is not easy to determine whether it is
$Z\subset [-1,1]^{n}\subset \mathbb{R}^{n}$, it is not easy to determine whether it is 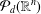 ${\mathcal{P}}_{d}(\mathbb{R}^{n})$-norming (here
${\mathcal{P}}_{d}(\mathbb{R}^{n})$-norming (here 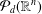 ${\mathcal{P}}_{d}(\mathbb{R}^{n})$ is the space of real polynomials of degree at most
${\mathcal{P}}_{d}(\mathbb{R}^{n})$ is the space of real polynomials of degree at most 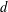 $d$ on
$d$ on 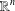 $\mathbb{R}^{n}$), that is, satisfies a Remez-type inequality:
$\mathbb{R}^{n}$), that is, satisfies a Remez-type inequality: 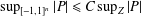 $\sup _{[-1,1]^{n}}|P|\leq C\sup _{Z}|P|$ for all
$\sup _{[-1,1]^{n}}|P|\leq C\sup _{Z}|P|$ for all 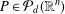 $P\in {\mathcal{P}}_{d}(\mathbb{R}^{n})$ with
$P\in {\mathcal{P}}_{d}(\mathbb{R}^{n})$ with 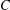 $C$ independent of
$C$ independent of 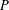 $P$. (Although
$P$. (Although 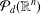 ${\mathcal{P}}_{d}(\mathbb{R}^{n})$-norming sets are precisely those not contained in any algebraic hypersurface of degree
${\mathcal{P}}_{d}(\mathbb{R}^{n})$-norming sets are precisely those not contained in any algebraic hypersurface of degree 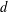 $d$ in
$d$ in 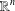 $\mathbb{R}^{n}$, there are many apparently unrelated reasons for
$\mathbb{R}^{n}$, there are many apparently unrelated reasons for 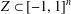 $Z\subset [-1,1]^{n}$ to have this property.) In the present paper we study norming sets and related Remez-type inequalities in a general setting of finite-dimensional linear spaces
$Z\subset [-1,1]^{n}$ to have this property.) In the present paper we study norming sets and related Remez-type inequalities in a general setting of finite-dimensional linear spaces 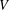 $V$ of continuous functions on
$V$ of continuous functions on 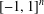 $[-1,1]^{n}$, remaining in most of the examples in the classical framework. First, we discuss some sufficient conditions for
$[-1,1]^{n}$, remaining in most of the examples in the classical framework. First, we discuss some sufficient conditions for 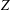 $Z$ to be
$Z$ to be 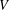 $V$-norming, partly known, partly new, restricting ourselves to the simplest nontrivial examples. Next, we extend the Turán–Nazarov inequality for exponential polynomials to several variables, and on this basis prove a new fewnomial Remez-type inequality. Finally, we study the family of optimal constants
$V$-norming, partly known, partly new, restricting ourselves to the simplest nontrivial examples. Next, we extend the Turán–Nazarov inequality for exponential polynomials to several variables, and on this basis prove a new fewnomial Remez-type inequality. Finally, we study the family of optimal constants 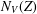 $N_{V}(Z)$ in the Remez-type inequalities for
$N_{V}(Z)$ in the Remez-type inequalities for 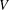 $V$, as the function of the set
$V$, as the function of the set 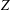 $Z$, showing that it is Lipschitz in the Hausdorff metric.
$Z$, showing that it is Lipschitz in the Hausdorff metric.