We prove a nonarchimedean analogue of Jørgensen’s inequality, and use it to deduce several algebraic convergence results. As an application, we show that every dense subgroup of 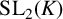 {\mathrm {SL}_2}(K), where K is a p-adic field, contains two elements that generate a dense subgroup of
{\mathrm {SL}_2}(K), where K is a p-adic field, contains two elements that generate a dense subgroup of 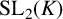 {\mathrm {SL}_2}(K), which is a special case of a result by Breuillard and Gelander [‘On dense free subgroups of Lie groups’, J. Algebra 261(2) (2003), 448–467]. We also list several other related results, which are well known to experts, but not easy to locate in the literature; for example, we show that a nonelementary subgroup of
{\mathrm {SL}_2}(K), which is a special case of a result by Breuillard and Gelander [‘On dense free subgroups of Lie groups’, J. Algebra 261(2) (2003), 448–467]. We also list several other related results, which are well known to experts, but not easy to locate in the literature; for example, we show that a nonelementary subgroup of 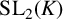 {\mathrm {SL}_2}(K) over a nonarchimedean local field K is discrete if and only if each of its two-generator subgroups is discrete.
{\mathrm {SL}_2}(K) over a nonarchimedean local field K is discrete if and only if each of its two-generator subgroups is discrete.