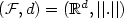1 results
Nearest neighbor classificationin infinite dimension
-
- Journal:
- ESAIM: Probability and Statistics / Volume 10 / February 2006
- Published online by Cambridge University Press:
- 08 September 2006, pp. 340-355
- Print publication:
- February 2006
-
- Article
- Export citation
-
Let X be a random element in a metric space (F,d), and let Y be a random variable with value 0 or 1. Y iscalled the class, or the label, of X. Let (Xi,Yi)1 ≤ i ≤ n be an observed i.i.d. sample having the same law as (X,Y). The problem of classification is topredict the label of a new random element X. The k-nearestneighbor classifier is the simple following rule: look atthe k nearest neighbors of X in the trial sample and choose 0 or 1 for its labelaccording to the majority vote. When $({\cal F},d)=(\mathbb{R}^d,||.||)$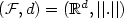
,Stone (1977) proved in 1977 the universal consistency of this classifier:its probability of error converges to the Bayes error, whatever thedistribution of (X,Y). We show in this paper that this result is nolonger valid in general metric spaces. However, if (F,d) isseparable and if some regularity condition is assumed, then thek-nearest neighbor classifier is weakly consistent.
