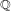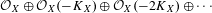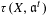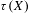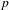Many results are known about test ideals and $F$-singularities for $\mathbb{Q}$-Gorenstein rings. In this paper, we generalize many of these results to the case when the symbolic Rees algebra ${\mathcal{O}}_{X}\oplus {\mathcal{O}}_{X}(-K_{X})\oplus {\mathcal{O}}_{X}(-2K_{X})\oplus \cdots \,$ is finitely generated (or more generally, in the log setting for $-K_{X}-\unicode[STIX]{x1D6E5}$). In particular, we show that the $F$-jumping numbers of $\unicode[STIX]{x1D70F}(X,\mathfrak{a}^{t})$ are discrete and rational. We show that test ideals $\unicode[STIX]{x1D70F}(X)$ can be described by alterations as in Blickle–Schwede–Tucker (and hence show that splinters are strongly $F$-regular in this setting – recovering a result of Singh). We demonstrate that multiplier ideals reduce to test ideals under reduction modulo $p$ when the symbolic Rees algebra is finitely generated. We prove that Hartshorne–Speiser–Lyubeznik–Gabber-type stabilization still holds. We also show that test ideals satisfy global generation properties in this setting.

We prove that certain roots of the Bernstein–Sato polynomial (i.e. $b$-function) are jumping coefficients up to a sign, showing a partial converse of a theorem of L. Ein, R. Lazarsfeld, K. E. Smith, and D. Varolin. We also prove that certain roots are determined by a filtration on the Milnor cohomology, generalizing a theorem of B. Malgrange in the isolated singularity case. This implies a certain relation with the spectrum which is determined by the Hodge filtration, because the above filtration is related to the pole order filtration. For multiplier ideals we prove an explicit formula in the case of locally conical divisors along a stratification, generalizing a formula of Mustaţ̌a in the case of hyperplane arrangements. We also give another proof of a formula of U. Walther on the $b$-function of a generic hyperplane arrangement, including the multiplicity of $-1$.

We introduce the notion of the Bernstein–Sato polynomial of an arbitrary variety (which is not necessarily reduced nor irreducible) using the theory of V-filtrations of M. Kashiwara and B. Malgrange. We prove that the decreasing filtration by multiplier ideals coincides essentially with the restriction of the V-filtration. This implies a relation between the roots of the Bernstein–Sato polynomial and the jumping coefficients of the multiplier ideals, and also a criterion for rational singularities in terms of the maximal root of the polynomial in the case of a reduced complete intersection. These are generalizations of the hypersurface case. We can calculate the polynomials explicitly in the case of monomial ideals.