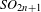1 results
THE DOUBLE COVER OF ODD GENERAL SPIN GROUPS, SMALL REPRESENTATIONS, AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 07 August 2015, pp. 609-671
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
-
We construct local and global metaplectic double covers of odd general spin groups, using the cover of Matsumoto of spin groups. Following Kazhdan and Patterson, a local exceptional representation is the unique irreducible quotient of a principal series representation, induced from a certain exceptional character. The global exceptional representation is obtained as the multi-residue of an Eisenstein series: it is an automorphic representation, and it decomposes as the restricted tensor product of local exceptional representations. As in the case of the small representation of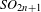
$\mathit{SO}_{2n+1}$ of Bump, Friedberg, and Ginzburg, exceptional representations enjoy the vanishing of a large class of twisted Jacquet modules (locally), or Fourier coefficients (globally). Consequently they are useful in many settings, including lifting problems and Rankin–Selberg integrals. We describe one application, to a calculation of a co-period integral.
