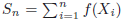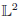Consider an irreducible, aperiodic and positive recurrent discrete time Markov chain(Xn,n ≥0) with invariant distribution μ. We shall investigate thelong time behaviour of some functionals of the chain, in particular the additivefunctional \hbox{$S_{n}=\sum_{i=1}^{n}f(X_{i})$}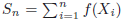${\mathit{S}}_{\mathit{n}}\mathrm{=}{\sum }_{\mathit{i}\mathrm{=}\mathrm{1}}^{\mathit{n}}\mathit{f}\mathrm{\left(}{\mathit{X}}_{\mathit{i}}\mathrm{\right)}$ for a possibly non square integrable functionf. To thisend we shall link ergodic properties of the chain to mixing properties, extending knownresults in the continuous time case. We will then use existing results of convergence tostable distributions, obtained in [M. Denker and A. Jakubowski, Stat. Probab.Lett. 8 (1989) 477–483; M. Tyran-Kaminska, StochasticProcess. Appl. 120 (2010) 1629–1650; D. Krizmanic, Ph.D. thesis(2010); B. Basrak, D. Krizmanic and J. Segers, Ann. Probab. 40(2012) 2008–2033] for stationary mixing sequences. Contrary to the usualL^2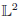$\mathrm{L}{\mathrm{2}}_{}^{}$ frameworkstudied in [P. Cattiaux, D. Chafai and A. Guillin, ALEA, Lat. Am. J. Probab. Math.Stat. 9 (2012) 337–382], where weak forms of ergodicity aresufficient to ensure the validity of the Central Limit Theorem, we will need here strongergodic properties: the existence of a spectral gap, hyperboundedness (orhypercontractivity). These properties are also discussed. Finally we give explicitexamples.

Starting from a sequence of independent Wright-Fisher diffusion processes on [0, 1], we construct a class of reversible infinite-dimensional diffusion processes on Δ∞ := {x ∈ [0, 1]N: ∑i≥1xi = 1} with GEM distribution as the reversible measure. Log-Sobolev inequalities are established for these diffusions, which lead to the exponential convergence of the corresponding reversible measures in the entropy. Extensions are made to a class of measure-valued processes over an abstract space S. This provides a reasonable alternative to the Fleming-Viot process, which does not satisfy the log-Sobolev inequality when S is infinite as observed by Stannat (2000).