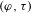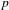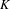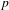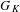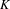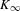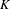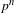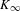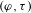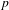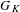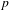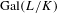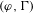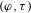1 results
LOCALLY ANALYTIC VECTORS AND OVERCONVERGENT
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D70F})$-MODULES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 03 May 2019, pp. 137-185
- Print publication:
- January 2021
-
- Article
- Export citation
-
Let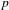
$p$ be a prime, let 
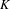$K$ be a complete discrete valuation field of characteristic 
$0$ with a perfect residue field of characteristic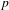 
$p$, and let 
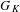$G_{K}$ be the Galois group. Let 
$\unicode[STIX]{x1D70B}$ be a fixed uniformizer of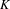 
$K$, let 
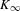$K_{\infty }$ be the extension by adjoining to 
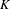$K$ a system of compatible 
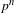$p^{n}$th roots of 
$\unicode[STIX]{x1D70B}$ for all 
$n$, and let 
$L$ be the Galois closure of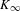 
$K_{\infty }$. Using these field extensions, Caruso constructs the 
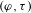$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D70F})$-modules, which classify 
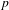$p$-adic Galois representations of 
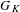$G_{K}$. In this paper, we study locally analytic vectors in some period rings with respect to the 
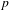$p$-adic Lie group 
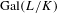$\operatorname{Gal}(L/K)$, in the spirit of the work by Berger and Colmez. Using these locally analytic vectors, and using the classical overconvergent 
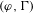$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$-modules, we can establish the overconvergence property of the 
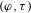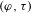$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D70F})$-modules.
