We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
This paper derives upper and lower bounds for the $\ell^p$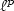 
-conditionnumber of the stiffness matrix resulting from the finite elementapproximation of a linear, abstract model problem. Sharp estimates interms of the meshsize h are obtained. The theoretical results areapplied to finite element approximations of elliptic PDE's invariational and in mixed form, and to first-order PDE's approximatedusing the Galerkin–Least Squares technique or bymeans of a non-standard Galerkin technique in L 1(Ω). Numerical simulations are presented to illustrate thetheoretical results.
