1 results
Spectral Properties of Schrödinger-type Operators andLarge-time Behavior of the Solutions to the Corresponding Wave Equation
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 1 / 2013
- Published online by Cambridge University Press:
- 28 January 2013, pp. 207-214
- Print publication:
- 2013
-
- Article
- Export citation
-
Let L be a linear, closed, densely defined in a Hilbert space operator,not necessarily selfadjoint. Consider the corresponding wave equations
\begin{eqnarray} &(1) \quad \ddot{w}+ Lw=0, \quadw(0)=0,\quad \dot{w}(0)=f, \quad \dot{w}=\frac{dw}{dt}, \quad f \in H. \\ &(2)\quad \ddot{u}+Lu=f e^{-ikt}, \quad u(0)=0, \quad \dot{u}(0)=0,\end{eqnarray}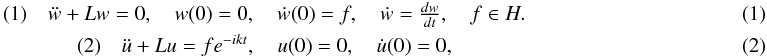
where k > 0 is a constant. Necessary and sufficient conditions aregiven for the operator L not to have eigenvalues in the half-planeRez < 0 and not to have a positive eigenvalue at a given point kd2 > 0. These conditions are given in terms of the large-timebehavior of the solutions to problem (1) for generic f.
Sufficient conditions are given for the validity of a version of the limiting amplitudeprinciple for the operator L.
A relation between the limiting amplitude principle and the limiting absorption principleis established.
