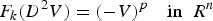1 results
On critical exponents of a k-Hessian equation in the whole space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 18 January 2019, pp. 1555-1575
- Print publication:
- December 2019
-
- Article
- Export citation
-
In this paper, we study negative classical solutions and stable solutions of the following k-Hessian equation
with radial structure, where n ⩾ 3, 1 < k < n/2 and p > 1. This equation is related to the extremal functions of the Hessian Sobolev inequality on the whole space. Several critical exponents including the Serrin type, the Sobolev type, and the Joseph-Lundgren type, play key roles in studying existence and decay rates. We believe that these critical exponents still come into play to research k-Hessian equations without radial structure.
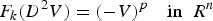$$F_k(D^2V) = (-V)^p\quad {\rm in}\;\; R^n$$
