1 results
JOINT DIAMONDS AND LAVER DIAMONDS
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 13 June 2019, pp. 895-928
- Print publication:
- September 2019
-
- Article
- Export citation
-
The concept of jointness for guessing principles, specifically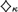
${\diamondsuit _\kappa }$ and various Laver diamonds, is introduced. A family of guessing sequences is joint if the elements of any given sequence of targets may be simultaneously guessed by the members of the family. While equivalent in the case of 
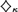${\diamondsuit _\kappa }$, joint Laver diamonds are nontrivial new objects. We give equiconsistency results for most of the large cardinals under consideration and prove sharp separations between joint Laver diamonds of different lengths in the case of θ-supercompact cardinals.
