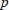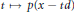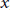Atmospheric flow equations govern the time evolution of chemical concentrations in theatmosphere. When considering gas and particle phases, the underlying partial differentialequations involve advection and diffusion operators, coagulation effects, and evaporationand condensation phenomena between the aerosol particles and the gas phase. Operatorsplitting techniques are generally used in global air quality models. When consideringorganic aerosol particles, the modeling of the thermodynamic equilibrium of each particleleads to the determination of the convex envelope of the energy function. Two strategiesare proposed to address the computation of convex envelopes. The first one is based on aprimal-dual interior-point method, while the second one relies on a variationalformulation, an appropriate augmented Lagrangian, an Uzawa iterative algorithm, and finiteelement techniques. Numerical experiments are presented for chemical systems ofatmospheric interest, in order to compute convex envelopes in various spacedimensions.

Interior-Point Methods (IPMs) are not only very effective in practice for solving linear optimization problems but also have polynomial-time complexity. Despite the practical efficiency of large-update algorithms, from a theoretical point of view, these algorithms have a weaker iteration bound with respect to small-update algorithms. In fact, there is a significant gap between theory and practice for large-update algorithms. By introducing self-regular barrier functions, Peng, Roos and Terlaky improved this gap up to a factor of log n. However, checking these self-regular functions is not simple and proofs of theorems involving these functions are very complicated. Roos el al. by presenting a new class of barrier functions which are not necessarily self-regular, achieved very good results through some much simpler theorems. In this paper we introduce a new kernel function in this class which yields the best known complexity bound, both for large-update and small-update methods.

A homogeneous real polynomial $p$ is hyperbolic with respect to a given vector $d$ if the univariate polynomial $t\,\mapsto \,p(x\,-\,td)$ has all real roots for all vectors $x$. Motivated by partial differential equations, Gårding proved in 1951 that the largest such root is a convex function of $x$, and showed various ways of constructing new hyperbolic polynomials. We present a powerful new such construction, and use it to generalize Gårding’s result to arbitrary symmetric functions of the roots. Many classical and recent inequalities follow easily. We develop various convex-analytic tools for such symmetric functions, of interest in interior-point methods for optimization problems over related cones.