1 results
Means in complete manifolds: uniqueness and approximation
-
- Journal:
- ESAIM: Probability and Statistics / Volume 18 / 2014
- Published online by Cambridge University Press:
- 27 March 2014, pp. 185-206
- Print publication:
- 2014
-
- Article
- Export citation
-
Let M be acomplete Riemannian manifold, M ∈ ℕ andp ≥ 1. Weprove that almost everywhere on x = (x1,...,xN) ∈ MNfor Lebesgue measure in MN, the measure \hbox{$\di \mu(x)=\f1N\sum_{k=1}^N\d_{x_k}$}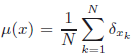
has a unique p–mean ep(x).As a consequence, if X = (X1,...,XN)is a MN-valued randomvariable with absolutely continuous law, then almost surely μ(X(ω)) has aunique p–mean. In particular if (Xn)n ≥ 1is an independent sample of an absolutely continuous law in M, then the processep,n(ω) = ep(X1(ω),...,Xn(ω))is well-defined. Assume M is compact and consider a probability measureν inM. Usingpartial simulated annealing, we define a continuous semimartingale which converges inprobability to the set of minimizers of the integral of distance at power p with respect toν. When theset is a singleton, it converges to the p–mean.
