1 results
Invariants of hyperplane groups and vanishing ideals of finite sets of points
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 16 March 2012, pp. 355-367
-
- Article
-
- You have access
- Export citation
-
We define a hyperplane group to be a finite group generated by reflections fixing a single hyperplane pointwise. Landweber and Stong proved that the invariant ring of a hyperplane group is again a polynomial ring in any characteristic. Recently, Hartmann and Shepler gave a constructive proof of this result. By their algorithm, one can always construct generators that are additive. In this paper, we study hyperplane groups of order a power of a prime p in characteristic p and give a slightly different construction of the generators than Hartmann and Shepler. We then show that such generators have a particular form. Furthermore, we show that if the group is defined by a finite additive subgroup W ⊆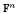
, the vanishing ideal of W is generated by polynomials obtained from a set of generators of the invariant ring that are additive. Finally, we give a shorter proof of the fact that the module of the invariant differential 1-forms is free in our situation.
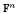, the vanishing ideal of 