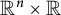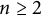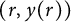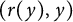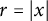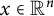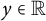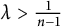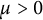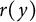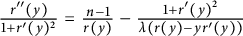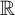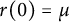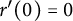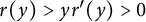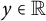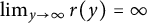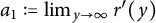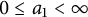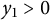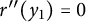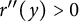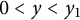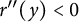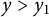We will give a new proof of the existence of hypercylinder expander of the inverse mean curvature flow which is a radially symmetric homothetic soliton of the inverse mean curvature flow in 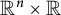 $\mathbb {R}^{n}\times \mathbb {R}$
,
$\mathbb {R}^{n}\times \mathbb {R}$
, 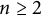 $n\ge 2$
, of the form
$n\ge 2$
, of the form 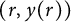 $(r,y(r))$
or
$(r,y(r))$
or 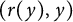 $(r(y),y)$
, where
$(r(y),y)$
, where 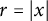 $r=|x|$
,
$r=|x|$
, 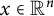 $x\in \mathbb {R}^{n}$
, is the radially symmetric coordinate and
$x\in \mathbb {R}^{n}$
, is the radially symmetric coordinate and 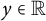 $y\in \mathbb {R}$
. More precisely, for any
$y\in \mathbb {R}$
. More precisely, for any 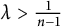 $\lambda>\frac {1}{n-1}$
and
$\lambda>\frac {1}{n-1}$
and 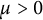 $\mu>0$
, we will give a new proof of the existence of a unique even solution
$\mu>0$
, we will give a new proof of the existence of a unique even solution 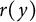 $r(y)$
of the equation
$r(y)$
of the equation 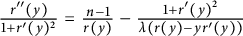 $\frac {r^{\prime \prime }(y)}{1+r^{\prime }(y)^{2}}=\frac {n-1}{r(y)}-\frac {1+r^{\prime }(y)^{2}}{\lambda (r(y)-yr^{\prime }(y))}$
in
$\frac {r^{\prime \prime }(y)}{1+r^{\prime }(y)^{2}}=\frac {n-1}{r(y)}-\frac {1+r^{\prime }(y)^{2}}{\lambda (r(y)-yr^{\prime }(y))}$
in 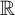 $\mathbb {R}$
which satisfies
$\mathbb {R}$
which satisfies 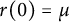 $r(0)=\mu $
,
$r(0)=\mu $
, 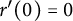 $r^{\prime }(0)=0$
and
$r^{\prime }(0)=0$
and 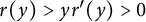 $r(y)>yr^{\prime }(y)>0$
for any
$r(y)>yr^{\prime }(y)>0$
for any 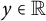 $y\in \mathbb {R}$
. We will prove that
$y\in \mathbb {R}$
. We will prove that 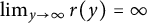 $\lim _{y\to \infty }r(y)=\infty $
and
$\lim _{y\to \infty }r(y)=\infty $
and 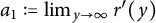 $a_{1}:=\lim _{y\to \infty }r^{\prime }(y)$
exists with
$a_{1}:=\lim _{y\to \infty }r^{\prime }(y)$
exists with 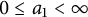 $0\le a_{1}<\infty $
. We will also give a new proof of the existence of a constant
$0\le a_{1}<\infty $
. We will also give a new proof of the existence of a constant 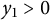 $y_{1}>0$
such that
$y_{1}>0$
such that 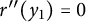 $r^{\prime \prime }(y_{1})=0$
,
$r^{\prime \prime }(y_{1})=0$
, 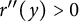 $r^{\prime \prime }(y)>0$
for any
$r^{\prime \prime }(y)>0$
for any 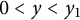 $0<y<y_{1}$
, and
$0<y<y_{1}$
, and 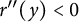 $r^{\prime \prime }(y)<0$
for any
$r^{\prime \prime }(y)<0$
for any 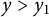 $y>y_{1}$
.
$y>y_{1}$
.