1 results
ORDINAL ANALYSIS OF PARTIAL COMBINATORY ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 10 June 2021, pp. 1154-1188
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
For every partial combinatory algebra (pca), we define a hierarchy of extensionality relations using ordinals. We investigate the closure ordinals of pca’s, i.e., the smallest ordinals where these relations become equal. We show that the closure ordinal of Kleene’s first model is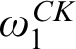
${\omega _1^{\textit {CK}}}$
and that the closure ordinal of Kleene’s second model is 
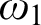$\omega _1$
. We calculate the exact complexities of the extensionality relations in Kleene’s first model, showing that they exhaust the hyperarithmetical hierarchy. We also discuss embeddings of pca’s.
