1 results
On the lifting of hermitian modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 5 / September 2008
- Published online by Cambridge University Press:
- 01 September 2008, pp. 1107-1154
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
-
Let K be an imaginary quadratic field with discriminant −D. We denote by 𝒪 the ring of integers of K. Let χ be the primitive Dirichlet character corresponding to K/ℚ. Let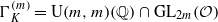
be the hermitian modular group of degree m. We construct a lifting from S2k(SL2(ℤ)) to S2k+2n(ΓK(2n+1),det −k−n) and a lifting from S2k+1(Γ0(D),χ) to S2k+2n(ΓK(2n),det −k−n). We give an explicit Fourier coefficient formula of the lifting. This is a generalization of the Maass lift considered by Kojima, Krieg and Sugano. We also discuss its extension to the adele group of U(m,m).
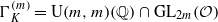be the hermitian modular group of degree 