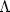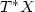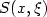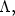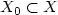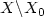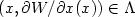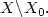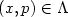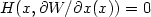1 results
Graph selectors and viscosity solutions on Lagrangian manifolds
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 12 / Issue 4 / October 2006
- Published online by Cambridge University Press:
- 11 October 2006, pp. 795-815
- Print publication:
- October 2006
-
- Article
- Export citation
-
Let $\Lambda $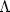
be a Lagrangian submanifold of $T^{*}X$ 
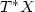for some closedmanifold X. Let $S(x,\xi )$ 
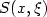be a generating function for $\Lambda $ 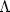whichis quadratic at infinity, and let W(x) be the corresponding graph selectorfor $\Lambda ,$ 
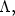in the sense of Chaperon-Sikorav-Viterbo, so that thereexists a subset $X_{0}\subset X$ 
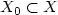of measure zero such that W is Lipschitzcontinuous on X, smooth on $X\backslash X_{0}$ 
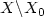and $(x,\partial W/\partialx(x))\in \Lambda $ 
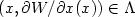for $X\backslash X_{0}.$ 
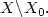Let H(x,p)=0 for $(x,p)\in\Lambda$ 
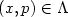. Then W is a classical solution to $H(x,\partial W/\partialx(x))=0$ 
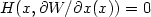on $X\backslash X_{0}$ 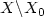and extends to a Lipschitz function on thewhole of X. Viterbo refers to W as a variational solution. We prove that W is also a viscosity solution under some simple and natural conditions.We also prove that these conditions are satisfied in many cases, includingcertain commonly occuring cases where H(x,p) is not convex in p.
