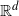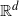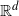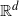We consider the Voronoi diagram generated by n independent and identically distributed $\mathbb{R}^{d}$ -valued random variables with an arbitrary underlying probability density function f on $\mathbb{R}^{d}$ , and analyze the asymptotic behaviors of certain geometric properties, such as the measure, of the Voronoi cells as n tends to infinity. We adapt the methods used by Devroye et al. (2017) to conduct a study of the asymptotic properties of two types of Voronoi cells: (1) Voronoi cells that have a fixed nucleus; (2) Voronoi cells that contain a fixed point. We show that the geometric properties of both types of cells resemble those in the case when the Voronoi diagram is generated by a homogeneous Poisson point process. Additionally, for the second type of Voronoi cells, we determine the limiting distribution, which is universal in all choices of f, of the re-scaled measure of the cells.