1 results
Functional limit theorems for the euler characteristic process in the critical regime
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 17 March 2021, pp. 57-80
- Print publication:
- March 2021
-
- Article
- Export citation
-
This study presents functional limit theorems for the Euler characteristic of Vietoris–Rips complexes. The points are drawn from a nonhomogeneous Poisson process on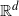
$\mathbb{R}^d$
, and the connectivity radius governing the formation of simplices is taken as a function of the time parameter t, which allows us to treat the Euler characteristic as a stochastic process. The setting in which this takes place is that of the critical regime, in which the simplicial complexes are highly connected and have nontrivial topology. We establish two ‘functional-level’ limit theorems, a strong law of large numbers and a central limit theorem, for the appropriately normalized Euler characteristic process.
