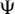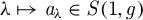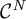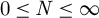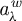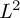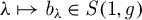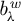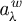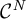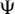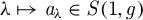The main result is that the ellipticity and the Fredholm property of a $\Psi $ DO acting on Sobolev spaces in the Weyl-Hörmander calculus are equivalent when the Hörmander metric is geodesically temperate and its associated Planck function vanishes at infinity. The proof is essentially related to the following result that we prove for geodesically temperate Hörmander metrics: If $\lambda \mapsto a_{\lambda }\in S(1,g)$ is a 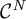$\mathcal {C}^N$ , 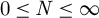$0\leq N\leq \infty $ , map such that each 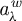$a_{\lambda }^w$ is invertible on 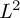$L^2$ , then the mapping 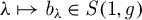$\lambda \mapsto b_{\lambda }\in S(1,g)$ , where 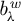$b_{\lambda }^w$ is the inverse of 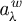$a_{\lambda }^w$ , is again of class $\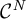mathcal {C}^N$ . Additionally, assuming also the strong uncertainty principle for the metric, we obtain a Fedosov-Hörmander formula for the index of an elliptic operator. At the very end, we give an example to illustrate our main result.