We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We prove some new structure results for automorphic products of singular weight. First, we give a simple characterisation of the Borcherds function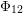 
$\unicode[STIX]{x1D6F7}_{12}$. Second, we show that holomorphic automorphic products of singular weight on lattices of prime level exist only in small signatures and we derive an explicit bound. Finally, we give a complete classification of reflective automorphic products of singular weight on lattices of prime level.
