1 results
The Hardy–Littlewood conjecture and rational points
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 10 September 2014, pp. 2095-2111
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
-
Schinzel’s Hypothesis (H) was used by Colliot-Thélène and Sansuc, and later by Serre, Swinnerton-Dyer and others, to prove that the Brauer–Manin obstruction controls the Hasse principle and weak approximation on pencils of conics and similar varieties. We show that when the ground field is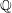
$\mathbb{Q}$ and the degenerate geometric fibres of the pencil are all defined over 
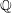$\mathbb{Q}$, one can use this method to obtain unconditional results by replacing Hypothesis (H) with the finite complexity case of the generalised Hardy–Littlewood conjecture recently established by Green, Tao and Ziegler.
