1 results
First passage upwards for state-dependent-killed spectrally negative Lévy processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 30 July 2019, pp. 472-495
- Print publication:
- June 2019
-
- Article
- Export citation
-
For a spectrally negative Lévy process X, killed according to a rate that is a function ω of its position, we complement the recent findings of [12] by analysing (in greater generality) the exit probability of the one-sided upwards passage problem. When ω is strictly positive, this problem is related to the determination of the Laplace transform of the first passage time upwards for X that has been time-changed by the inverse of the additive functional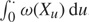
$$\int_0^ \cdot \omega ({X_u}){\kern 1pt} {\rm{d}}u$$. In particular, our findings thus shed extra light on related results concerning first passage times downwards (resp. upwards) of continuous-state branching processes (resp. spectrally negative positive self-similar Markov processes).
