Savin [‘ 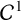$\mathcal {C}^{1}$ regularity for infinity harmonic functions in two dimensions’, Arch. Ration. Mech. Anal. 3(176) (2005), 351–361] proved that every planar absolutely minimizing Lipschitz (AML) function is continuously differentiable whenever the ambient space is Euclidean. More recently, Peng et al. [‘Regularity of absolute minimizers for continuous convex Hamiltonians’, J. Differential Equations 274 (2021), 1115–1164] proved that this property remains true for planar AML functions for certain convex Hamiltonians, using some Euclidean techniques. Their result can be applied to AML functions defined in two-dimensional normed spaces with differentiable norm. In this work we develop a purely non-Euclidean technique to obtain the regularity of planar AML functions in two-dimensional normed spaces with differentiable norm.