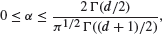1 results
Isotropic correlation functions on d-dimensional balls
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 625-631
- Print publication:
- September 1999
-
- Article
- Export citation
-
A popular procedure in spatial data analysis is to fit a line segment of the form c(x) = 1 - α ||x||, ||x|| < 1, to observed correlations at (appropriately scaled) spatial lag x in d-dimensional space. We show that such an approach is permissible if and only if
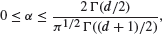
the upper bound depending on the spatial dimension d. The proof relies on Matheron's turning bands operator and an extension theorem for positive definite functions due to Rudin. Side results and examples include a general discussion of isotropic correlation functions defined on d-dimensional balls.
