We study analytic properties function 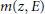 $m\left( z,\,E \right)$, which is defined on the upper half-plane as an integral from the shifted
$m\left( z,\,E \right)$, which is defined on the upper half-plane as an integral from the shifted 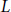 $L$-function of an elliptic curve. We show that
$L$-function of an elliptic curve. We show that 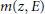 $m\left( z,\,E \right)$ analytically continues to a meromorphic function on the whole complex plane and satisfies certain functional equation. Moreover, we give explicit formula for
$m\left( z,\,E \right)$ analytically continues to a meromorphic function on the whole complex plane and satisfies certain functional equation. Moreover, we give explicit formula for 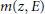 $m\left( z,\,E \right)$ in the strip
$m\left( z,\,E \right)$ in the strip  $\left| \Im z \right|\,<\,2\pi$.
$\left| \Im z \right|\,<\,2\pi$.