1 results
A priori bounds and multiplicity of positive solutions for p-Laplacian Neumann problems with sub-critical growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 73-102
- Print publication:
- February 2020
-
- Article
- Export citation
-
Let 1 < p < +∞ and let Ω ⊂ ℝN be either a ball or an annulus. We continue the analysis started in [Boscaggin, Colasuonno, Noris, ESAIM Control Optim. Calc. Var. (2017)], concerning quasilinear Neumann problems of the type
We suppose that f(0) = f(1) = 0 and that f is negative between the two zeros and positive after. In case Ω is a ball, we also require that f grows less than the Sobolev-critical power at infinity. We prove a priori bounds of radial solutions, focussing in particular on solutions which start above 1. As an application, we use the shooting technique to get existence, multiplicity and oscillatory behaviour (around 1) of non-constant radial solutions.
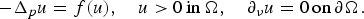$-\Delta _pu = f(u),\quad u > 0\,{\rm in }\,\Omega ,\quad \partial _\nu u = 0\,{\rm on }\,\partial \Omega .$
