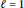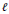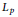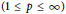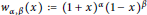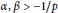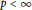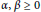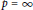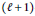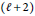In this paper, we prove that for
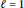 $\ell \,=\,1$
or 2 the rate of best
$\ell \,=\,1$
or 2 the rate of best
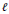 $\ell $
- monotone polynomial approximation in the
$\ell $
- monotone polynomial approximation in the
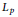 ${{L}_{p}}$
norm
${{L}_{p}}$
norm
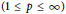 $\left( 1\,\le \,p\,\le \,\infty \right)$
weighted by the Jacobi weight
$\left( 1\,\le \,p\,\le \,\infty \right)$
weighted by the Jacobi weight
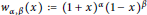 ${{w}_{\alpha ,\,\beta }}\left( x \right)\,:=\,{{\left( 1\,+\,x \right)}^{\alpha }}{{\left( 1\,-\,x \right)}^{\beta }}$
with
${{w}_{\alpha ,\,\beta }}\left( x \right)\,:=\,{{\left( 1\,+\,x \right)}^{\alpha }}{{\left( 1\,-\,x \right)}^{\beta }}$
with
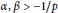 $\alpha ,\,\beta \,>\,-1/p$
if
$\alpha ,\,\beta \,>\,-1/p$
if
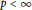 $p\,<\,\infty $
, or
$p\,<\,\infty $
, or
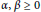 $\alpha ,\,\beta \,\ge \,0$
if
$\alpha ,\,\beta \,\ge \,0$
if
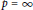 $p\,=\,\infty $
, is bounded by an appropriate
$p\,=\,\infty $
, is bounded by an appropriate
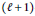 $\left( \ell \,+\,1 \right)$
-st modulus of smoothness with the same weight, and that this rate cannot be bounded by the
$\left( \ell \,+\,1 \right)$
-st modulus of smoothness with the same weight, and that this rate cannot be bounded by the
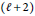 $\left( \ell \,+\,2 \right)$
-nd modulus. Related results on constrained weighted spline approximation and applications of our estimates are also given.
$\left( \ell \,+\,2 \right)$
-nd modulus. Related results on constrained weighted spline approximation and applications of our estimates are also given.