We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The famous five halves theorem of Boardman states that, if T: Mm → Mm is a smooth involution defined on a non-bounding closed smooth m-dimensional manifold Mm (m > 1) and if
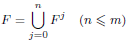
is the fixed-point set of T, where Fj denotes the union of those components of F having dimension j, then 2m ≤ 5n. If the dimension m is written as m = 5k − c, where k ≥ 1 and 0 ≤ c < 5, the theorem states that the dimension n of the fixed submanifold is at least β(m), where β(m) = 2k if c = 0, 1, 2 and β(m) = 2k − 1 if c = 3, 4. In this paper, we give, for each m > 1, the equivariant cobordism classification of involutions (Mm, T), for which the fixed submanifold F attains the minimal dimension β(m).
