In this paper, we study the power and limitations of computing effectively generic sequences using effectively random oracles. Previously, it was known that every 2-random sequence computes a 1-generic sequence (as shown by Kautz) and every 2-random sequence forms a minimal pair in the Turing degrees with every 2-generic sequence (as shown by Nies, Stephan, and Terwijn). We strengthen these results by showing that every Demuth random sequence computes a 1-generic sequence and that every Demuth random sequence forms a minimal pair with every pb-generic sequence (where pb-genericity is an effective notion of genericity that is strictly between 1-genericity and 2-genericity). Moreover, we prove that for every comeager 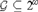 ${\cal G} \subseteq {2^\omega }$, there is some weakly 2-random sequence X that computes some
${\cal G} \subseteq {2^\omega }$, there is some weakly 2-random sequence X that computes some 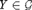 $Y \in {\cal G}$, a result that allows us to provide a fairly complete classification as to how various notions of effective randomness interact in the Turing degrees with various notions of effective genericity.
$Y \in {\cal G}$, a result that allows us to provide a fairly complete classification as to how various notions of effective randomness interact in the Turing degrees with various notions of effective genericity.