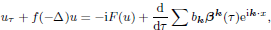We consider the free linear Schrödinger equation on a torus 𝕋d, perturbed by a Hamiltonian nonlinearity, driven by a random force and subject to a linear damping:
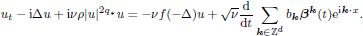
Here u = u(t, x), x ∈ 𝕋d, 0 < ν ≪ 1, q∗ ∈ ℕ, f is a positive continuous function, ρ is a positive parameter and 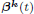 are standard independent complex Wiener processes. We are interested in limiting, as ν → 0, behaviour of distributions of solutions for this equation and of its stationary measure. Writing the equation in the slow time τ = νt, we prove that the limiting behaviour of them both is described by the effective equation
are standard independent complex Wiener processes. We are interested in limiting, as ν → 0, behaviour of distributions of solutions for this equation and of its stationary measure. Writing the equation in the slow time τ = νt, we prove that the limiting behaviour of them both is described by the effective equation
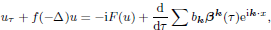
where the nonlinearity F(u) is made out of the resonant terms of the monomial |u|2q∗u.

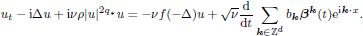
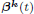 are standard independent complex Wiener processes. We are interested in limiting, as
are standard independent complex Wiener processes. We are interested in limiting, as