Recently Ovsienko and Tabachnikov considered extensions of Somos and Gale-Robinson sequences, defined over the algebra of dual numbers. Ovsienko used the same idea to construct so-called shadow sequences derived from other nonlinear recurrence relations exhibiting the Laurent phenomenon, with the original motivation being the hope that these examples should lead to an appropriate notion of a cluster superalgebra, incorporating Grassmann variables. Here, we present various explicit expressions for the shadow of Somos-4 sequences and describe the solution of a general Somos-4 recurrence defined over the 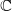$\mathbb{C}$ -algebra of dual numbers from several different viewpoints: analytic formulae in terms of elliptic functions, linear difference equations, and Hankel determinants.

In this work we investigate the internal syntax and semantics of quantifier phrases (QP) involving cardinal numerals. Concentrating on a set of previously documented puzzles concerning Case and number agreement within the numeral phrase in Russian, we argue that these agreement patterns follow naturally if one recognizes three structural layers in a numeral-based QP: the countability layer, the number layer and the quantificational layer. Our central theoretical claim is that the countability layer is implemented as a (pseudo-)classifier structure whose morphological manifestation obeys a principle of syntactic ‘visibility’. Our specific claim for Russian is that, diachronically, this countability layer has emerged as a result of the loss of the dual number in the course of transition between Old and Modern Russian. We strengthen our conclusions with psycholinguistic evidence from a sentence completion study that tests Russian speakers’ sensitivity to the countability layer.