We propose a variation of the classical Hilbert scheme of points, the double nested Hilbert scheme of points, which parametrizes flags of zero-dimensional subschemes whose nesting is dictated by a Young diagram. Over a smooth quasi-projective curve, we compute the generating series of topological Euler characteristic of these spaces, by exploiting the combinatorics of reversed plane partitions. Moreover, we realize this moduli space as the zero locus of a section of a vector bundle over a smooth ambient space, which therefore admits a virtual fundamental class. We apply this construction to the stable pair theory of a local curve, that is the total space of the direct sum of two line bundles over a curve. We show that the invariants localize to virtual intersection numbers on double nested Hilbert scheme of points on the curve, and that the localized contributions to the invariants are controlled by three universal series for every Young diagram, which can be explicitly determined after the anti-diagonal restriction of the equivariant parameters. Under the anti-diagonal restriction, the invariants are matched with the Gromov–Witten invariants of local curves of Bryan–Pandharipande, as predicted by the Maulik–Nekrasov–Okounkov–Pandharipande (MNOP) correspondence. Finally, we discuss 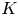 $K$-theoretic refinements à la Nekrasov–Okounkov.
$K$-theoretic refinements à la Nekrasov–Okounkov.