This paper is concerned with the structure of asymptotically stabilizing feedbacks for a nonlinear control system on $\mathbb{R}^n$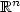. We first introduce a family of discontinuous, piecewise smooth vector fields and derive a number of properties enjoyed by solutions of the corresponding O.D.E's. We then define a class of “patchy feedbacks” which are obtained by patching together a locally finite family of smooth controls. Our main result shows that, if a system is asymptotically controllable at the origin, then it can be stabilized by a piecewise constant patchy feedback control.