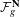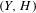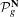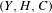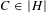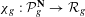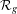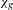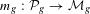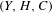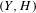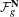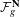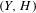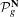Let ${\mathcal{F}}_{g}^{\mathbf{N}}$ be the moduli space of polarized Nikulin surfaces $(Y,H)$ of genus $g$ and let ${\mathcal{P}}_{g}^{\mathbf{N}}$ be the moduli of triples 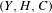$(Y,H,C)$, with 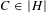$C\in |H|$ a smooth curve. We study the natural map 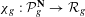$\unicode[STIX]{x1D712}_{g}:{\mathcal{P}}_{g}^{\mathbf{N}}\rightarrow {\mathcal{R}}_{g}$, where 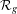${\mathcal{R}}_{g}$ is the moduli space of Prym curves of genus $g$. We prove that it is generically injective on every irreducible component, with a few exceptions in low genus. This gives a complete picture of the map 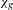$\unicode[STIX]{x1D712}_{g}$ and confirms some striking analogies between it and the Mukai map 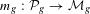$m_{g}:{\mathcal{P}}_{g}\rightarrow {\mathcal{M}}_{g}$ for moduli of triples 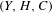$(Y,H,C)$, where 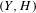$(Y,H)$ is any genus $g$ polarized $K3$ surface. The proof is by degeneration to boundary points of a partial compactification of 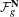${\mathcal{F}}_{g}^{\mathbf{N}}$. These represent the union of two surfaces with four even nodes and effective anticanonical class, which we call half Nikulin surfaces. The use of this degeneration is new with respect to previous techniques.

Let A be a finite-dimensional k-algebra over algebraically closed field k and $m{\rm mod}\, A$ be the category of finite-dimensional left A-modules. We show that a module M in ${\rm mod}\, A$ degenerates to another module N in ${\rm mod}\, A$ if and only if there is an exact sequence $0\to N\to M\oplus Z\to Z\to 0$ in ${\rm mod}\, A$ for some A-module Z. Moreover, we give a description of minimal degenerations of finite-dimensional A-modules.