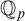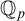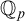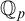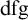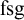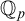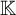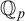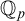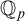The aim of this paper is to develop the theory of groups definable in the p-adic field 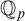 ${{\mathbb {Q}}_p}$, with “definable f-generics” in the sense of an ambient saturated elementary extension of
${{\mathbb {Q}}_p}$, with “definable f-generics” in the sense of an ambient saturated elementary extension of 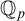 ${{\mathbb {Q}}_p}$. We call such groups definable f-generic groups.
${{\mathbb {Q}}_p}$. We call such groups definable f-generic groups.
So, by a “definable f-generic” or 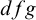 $dfg$ group we mean a definable group in a saturated model with a global f-generic type which is definable over a small model. In the present context the group is definable over
$dfg$ group we mean a definable group in a saturated model with a global f-generic type which is definable over a small model. In the present context the group is definable over 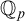 ${{\mathbb {Q}}_p}$, and the small model will be
${{\mathbb {Q}}_p}$, and the small model will be 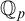 ${{\mathbb {Q}}_p}$ itself. The notion of a
${{\mathbb {Q}}_p}$ itself. The notion of a 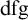 $\mathrm {dfg}$ group is dual, or rather opposite to that of an
$\mathrm {dfg}$ group is dual, or rather opposite to that of an 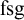 $\operatorname {\mathrm {fsg}}$ group (group with “finitely satisfiable generics”) and is a useful tool to describe the analogue of torsion-free o-minimal groups in the p-adic context.
$\operatorname {\mathrm {fsg}}$ group (group with “finitely satisfiable generics”) and is a useful tool to describe the analogue of torsion-free o-minimal groups in the p-adic context.
In the current paper our group will be definable over 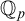 ${{\mathbb {Q}}_p}$ in an ambient saturated elementary extension
${{\mathbb {Q}}_p}$ in an ambient saturated elementary extension 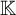 $\mathbb {K}$ of
$\mathbb {K}$ of 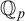 ${{\mathbb {Q}}_p}$, so as to make sense of the notions of f-generic type, etc. In this paper we will show that every definable f-generic group definable in
${{\mathbb {Q}}_p}$, so as to make sense of the notions of f-generic type, etc. In this paper we will show that every definable f-generic group definable in 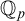 ${{\mathbb {Q}}_p}$ is virtually isomorphic to a finite index subgroup of a trigonalizable algebraic group over
${{\mathbb {Q}}_p}$ is virtually isomorphic to a finite index subgroup of a trigonalizable algebraic group over 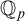 ${{\mathbb {Q}}_p}$. This is analogous to the o-minimal context, where every connected torsion-free group definable in
${{\mathbb {Q}}_p}$. This is analogous to the o-minimal context, where every connected torsion-free group definable in 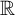 $\mathbb {R}$ is isomorphic to a trigonalizable algebraic group [5, Lemma 3.4]. We will also show that every open definable f-generic subgroup of a definable f-generic group has finite index, and every f-generic type of a definable f-generic group is almost periodic, which gives a positive answer to the problem raised in [28] of whether f-generic types coincide with almost periodic types in the p-adic case.
$\mathbb {R}$ is isomorphic to a trigonalizable algebraic group [5, Lemma 3.4]. We will also show that every open definable f-generic subgroup of a definable f-generic group has finite index, and every f-generic type of a definable f-generic group is almost periodic, which gives a positive answer to the problem raised in [28] of whether f-generic types coincide with almost periodic types in the p-adic case.