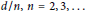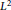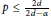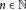1 results
Convolution Powers of Salem Measures With Applications
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 2 / 01 April 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 284-320
- Print publication:
- 01 April 2017
-
- Article
-
- You have access
- Export citation
-
We study the regularity of convolution powers for measures supported on Salem sets, and prove related results on Fourier restriction and Fourier multipliers. In particular we show that for
$\alpha $ of the form 
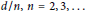$d\,/\,n,\,n\,=\,2,3,...$ there exist $\alpha $-Salem measures for which the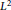 
${{L}^{2}}$ Fourier restriction theorem holds in the range 
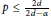$p\,\le \,\frac{2d}{2d\,-\,\alpha }$. The results rely on ideas of Körner. We extend some of his constructions to obtain upper regular $\alpha $-Salem measures, with sharp regularity results for 
$n$-fold
convolutions for all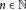 
$n\,\in \,\mathbb{N}$.
