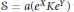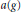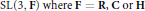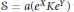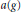In this paper, we consider the set $\text{S}=a\left( {{e}^{X}}K{{e}^{Y}} \right)$ where $a\left( g \right)$ is the abelian part in the Cartan decomposition of $g$. This is exactly the support of the measure intervening in the product formula for the spherical functions on symmetric spaces of noncompact type. We give a simple description of that support in the case of 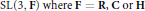$\text{SL}\left( 3,\,\mathbf{F} \right)\,\text{where}\,\mathbf{F}\,=\,\mathbf{R},\,\mathbf{C}\,\text{or}\,\mathbf{H}$. In particular, we show that $\text{S}$ is convex.

We also give an application of our result to the description of singular values of a product of two arbitrary matrices with prescribed singular values.

The summability fields of generalized Nörlund means (N,p*α,p), α ∈ Ν, are increasing with a and are contained in that of the corresponding power series method (P,p). Particular cases are the Cesàro- and Euler-means with corresponding power series methods of Abel and Borel. In this paper we generalize a convexity theorem, which is well-known for the Cesàro means and which was recently shown for the Euler means to a large class of generalized Nörlund means.