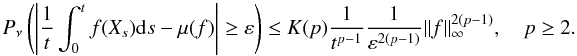1 results
Polynomial deviation bounds for recurrent Harris processeshaving general state space
-
- Journal:
- ESAIM: Probability and Statistics / Volume 17 / 2013
- Published online by Cambridge University Press:
- 08 February 2013, pp. 195-218
- Print publication:
- 2013
-
- Article
- Export citation
-
Consider a strong Markov process in continuous time, taking values in some Polish statespace. Recently, Douc et al. [Stoc. Proc. Appl.119, (2009) 897–923] introduced verifiable conditions in terms ofa supermartingale property implying an explicit control of modulated moments of hittingtimes. We show how this control can be translated into a control of polynomial moments ofabstract regeneration times which are obtained by using the regeneration method ofNummelin, extended to the time-continuous context. As a consequence, if ap-th moment of the regeneration times exists, we obtain non asymptoticdeviation bounds of the form
\begin{equation*} P_{\nu} \left(\left|\frac1t\int_0^tf(X_s){\rm d}s-\mu(f)\right|\geq\ge\right)\leqK(p)\frac1{t^{p- 1}}\frac 1{\ge^{2(p-1)}}\|f\|_\infty^{2(p-1)} ,\quad p \geq 2.\end{equation*}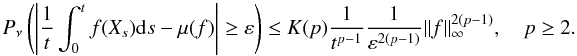Here, f is a bounded function andμ is the invariant measure of the process. We give several examples,including elliptic stochastic differential equations and stochastic differential equationsdriven by a jump noise.
