We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We introduce a wide subclass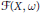 
$\mathcal{F}\left( X,\,\omega \right)$ of quasi-plurisubharmonic functions in a compact Kähler manifold, on which the complex Monge-Ampère operator is well defined and the convergence theorem is valid. We also prove that 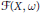$\mathcal{F}\left( X,\,\omega \right)$ is a convex cone and includes all quasi-plurisubharmonic functions that are in the Cegrell class.
