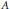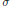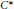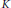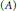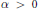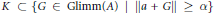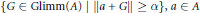1 results
Compact Subsets of the Glimm Space of a C*-algebra
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 1 / 14 March 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 90-96
- Print publication:
- 14 March 2014
-
- Article
-
- You have access
- Export citation
-
If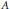
$A$ is a 
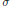$\sigma $-unital 
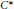${{C}^{*}}$-algebra and 
$a$ is a strictly positive element of 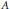$A$, then for every compact subset 
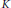$K$ of the complete regularization Glimm
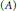$(A)$ of Prim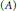$(A)$ there exists 
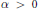$\alpha \,>\,0$ such that 
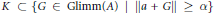$K\,\subset \,\{G\,\in \,\text{Glimm(}A\text{)}\,\text{ }\!\!|\!\!\text{ }\,\left\| a\,+\,G \right\|\,\ge \,\alpha \}$. This extends a result of J. Dauns to all 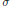$\sigma $-unital 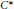${{C}^{*}}$-algebras. However, there exist a 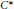${{C}^{*}}$-algebra 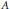$A$ and a compact subset of Glimm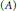$(A)$ that is not contained in any set of the form 
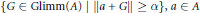$\{G\,\in \,\text{Glimm(}A\text{)}\,\text{ }\!\!|\!\!\text{ }\,\left\| a+\,G \right\|\,\ge \,\alpha \},\,a\in \,A$ and 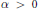$\alpha \,>\,0$.
