1 results
Convergence Rates of Cascade Algorithms with Infinitely Supported Masks
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 2 / 01 June 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 424-434
- Print publication:
- 01 June 2012
-
- Article
-
- You have access
- Export citation
-
We investigate the solutions of refinement equations of the form
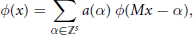$$\phi (x)\,=\,\sum\limits_{\alpha \in {{\mathbb{Z}}^{S}}}{a(\alpha )\,}\phi (Mx\,-\,\alpha ),$$where the function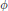
$\phi $ is in 
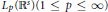${{L}_{p}}({{\mathbb{R}}^{s}})(1\,\le \,p\,\le \,\infty )$, 
$a$ is an infinitely supported sequence on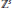 
${{\mathbb{Z}}^{s}}$ called a refinement mask, and 
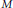$M$ is an 
$s\,\times \,s$ integer matrix such that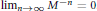 
${{\lim }_{n\to \infty }}\,{{M}^{-n}}\,=\,0$. Associated with the mask $a$ and 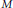$M$ is a linear operator 
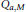${{\text{Q}}_{a,M}}$ defined on 
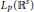${{L}_{p}}({{\mathbb{R}}^{s}})$ by 
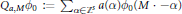${{\text{Q}}_{a,M}}{{\phi }_{0}}\,:=\,{{\sum }_{\alpha \in {{\mathbb{Z}}^{s}}}}\,a(\alpha ){{\phi }_{0}}(M\,\cdot \,-\alpha )$. Main results of this paper are related to the convergence rates of 
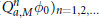${{(\text{Q}_{a,M}^{n}{{\phi }_{o}})}_{n=1,2,\ldots }}$ in 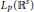${{L}_{p}}({{\mathbb{R}}^{s}})$ with mask $a$ being infinitely supported. It is proved that under some appropriate conditions on the initial function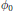 
${{\phi }_{0}}$, 
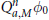$\text{Q}_{a,M}^{n}{{\phi }_{0}}$ converges in 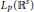${{L}_{p}}({{\mathbb{R}}^{s}})$ with an exponential rate.
