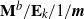 $\mathbf{M}^{b}/\mathbf{E}_{k}/1/\textbf{m}$
,
$\mathbf{M}^{b}/\mathbf{E}_{k}/1/\textbf{m}$
, 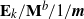 $\mathbf{E}_{k}/\mathbf{M}^{b}/1/\textbf{m}$
, and related queues
$\mathbf{E}_{k}/\mathbf{M}^{b}/1/\textbf{m}$
, and related queues