A class of graphs is bridge-addable if given a graph 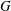 $G$ in the class, any graph obtained by adding an edge between two connected components of
$G$ in the class, any graph obtained by adding an edge between two connected components of  $G$ is also in the class. The authors recently proved a conjecture of McDiarmid, Steger, and Welsh stating that if
$G$ is also in the class. The authors recently proved a conjecture of McDiarmid, Steger, and Welsh stating that if 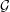 ${\mathcal{G}}$ is bridge-addable and
${\mathcal{G}}$ is bridge-addable and 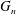 $G_{n}$ is a uniform
$G_{n}$ is a uniform  $n$-vertex graph from
$n$-vertex graph from 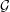 ${\mathcal{G}}$, then
${\mathcal{G}}$, then 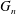 $G_{n}$ is connected with probability at least
$G_{n}$ is connected with probability at least 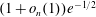 $(1+o_{n}(1))e^{-1/2}$. The constant
$(1+o_{n}(1))e^{-1/2}$. The constant 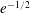 $e^{-1/2}$ is best possible, since it is reached for the class of all forests.
$e^{-1/2}$ is best possible, since it is reached for the class of all forests.
In this paper, we prove a form of uniqueness in this statement: if 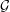 ${\mathcal{G}}$ is a bridge-addable class and the random graph
${\mathcal{G}}$ is a bridge-addable class and the random graph 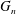 $G_{n}$ is connected with probability close to
$G_{n}$ is connected with probability close to 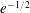 $e^{-1/2}$, then
$e^{-1/2}$, then 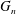 $G_{n}$ is asymptotically close to a uniform
$G_{n}$ is asymptotically close to a uniform  $n$-vertex random forest in a local sense. For example, if the probability converges to
$n$-vertex random forest in a local sense. For example, if the probability converges to 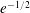 $e^{-1/2}$, then
$e^{-1/2}$, then 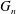 $G_{n}$ converges in the sense of Benjamini–Schramm to the uniformly infinite random forest
$G_{n}$ converges in the sense of Benjamini–Schramm to the uniformly infinite random forest 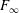 $F_{\infty }$. This result is reminiscent of so-called “stability results” in extremal graph theory, the difference being that here the stable extremum is not a graph but a graph class.
$F_{\infty }$. This result is reminiscent of so-called “stability results” in extremal graph theory, the difference being that here the stable extremum is not a graph but a graph class.