1 results
Which special functions of bounded deformation have bounded variation?
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 33-50
- Print publication:
- February 2018
-
- Article
- Export citation
-
Functions of bounded deformation (BD) arise naturally in the study of fracture and damage in a geometrically linear context. They are related to functions of bounded variation (BV), but are less well understood. We discuss here the relation to BV under additional regularity assumptions, which may require the regular part of the strain to have higher integrability or the jump set to have finite area or the Cantor part to vanish. On the positive side, we prove that BD functions that are piecewise affine on a Caccioppoli partition are in GSBV, and we prove that SBDp functions are approximately continuous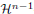
-almost everywhere away from the jump set. On the negative side, we construct a function that is BD but not in BV and has distributional strain consisting only of a jump part, and one that has a distributional strain consisting of only a Cantor part.
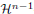-almost everywhere away from the jump set. On the negative side, we construct a function that is BD but not in BV and has distributional strain consisting only of a jump part, and one that has a distributional strain consisting of only a Cantor part.