We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
As an analog of a well-known theoremon the bilinear fractional integral on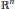 
${{\mathbb{R}}^{n}}$ by Kenig and Stein, we establish the similar boundedness property for a bilinear fractional integral on a compact Lie group. Our result is also a generalization of our recent theorem about the bilinear fractional integral on torus.
